Trajectory planning and control

A wide class of nonlinear control systems can be described by an ordinary differential equation which is affine in the controls:

$$\dot{x}=f_0(x)u_0+f_1(x)u_1+\ldots+f_m(x)u_m=f(x,u)~$$ (15)

where $x\in\mathcal{M}$ is the state of the system, $\mathcal{M}$ is the manifold on which the system evolves, $f_i:\mathcal{M}\rightarrow T\mathcal{M}$, $i=0,1,\ldots,m$, are analytic vector fields defined on $\mathcal{M}$, and $u_i\in\mathbb{R}$, $i=0,1,\ldots,m$, are scalar, measurable, control functions. The control problem for (15), with $u\stackrel{def}{=}[u_0,u_1,\ldots,u_m]\in\mathbb{R}^{m+1}$, becomes challenging if $m+1<n$. Equation (15) can be thought to represent both driftless systems, and systems with drift (if $u_0=1$). Practical examples can be found in [32,27,35] and include robotic manipulators, mobile robots, underwater vehicles, and rigid bodies in space. With reference to systems described by (15), the theory of Lie algebras and groups is known to be helpful in the following:

• Establishing the controllability properties of the system.
• Developing control laws that stabilize the system to a given equilibrium point, or ensure tracking of a desired reference trajectory.

Chow's Theorem delivers a conclusive result for the determination of complete controllability for driftless system (15). Chow's result involves the verification of the Lie algebra rank condition (LARC), see [32]:

$$L(f_0,f_1,\ldots,f_m)(p) = T_pM$$ (16)

for any $p\in M$, where $L(f_0,f_1,\ldots,f_m)(p) \stackrel{def}{=} \mathrm{span}\{f(p)\in T_p M\vert f\in L(f_0,f_1,\ldots,f_m)\}$ and $T_p M$ is the tangent space to $M$ at $p$. The LARC hence requires the construction of a spanning set (ideally a basis) for the Lie algebra of vector fields $L(f_0,f_1,\ldots,f_m)$. To this end the LTP package is used as follows. For a sufficiently large $k$, a Hall basis $\{B_1,B_2,\ldots,B_r\}$ is first generated for $L_k(\bar{X}_{m+1})$ and then each Lie product $B_i$, $i=1,2,\ldots,r$ of this basis is mapped into a corresponding Lie product of vector fields in $L(f_0,f_1,\ldots,f_m)$ by using the evaluation map, defined by $Ev:X_{i}\rightarrow f_i$, for $i=0,1,\ldots,m$, which assigns $f_i$ to $X_i$, $i=0,1,\ldots,m$, in any formal Lie product $B_i$, $i=1,2,\ldots,r$. The evaluation map becomes the canonical Lie algebra homomorphism if $L(f_0,f_1,\ldots,f_m)=L_k(f_0,f_1,\ldots,f_m)$, i.e. when $L(f_0,f_1,\ldots,f_m)$ is nilpotent. For systems with drift the LARC only ensures accessibility of the system, i.e. that the reachable set at any $p\in M$ has a non-empty interior, see [32]. The computation of a basis for $L(f_0,f_1,\ldots,f_m)$ is however still useful since the dimension of the set $L(f_0,f_1,\ldots,f_m)(p)$ and the highest order of the Lie products appearing in $L(f_0,f_1,\ldots,f_m)(p)$ reveal the difficulty of controlling (15). Assuming that system (15) is completely controllable, a variety of Lie algebraic-based control synthesis methods have been proposed in the literature, see for example [27,32]. Pivotal to controllability considerations, the design, and the derivation of control strategies for system (15) is the capability to generate equivalent system motions in directions outside the span of the vector fields $f_i$, $i=0,1,\ldots,m$. For simplicity of exposition, assume at first that piece-wise constant switching controls are employed for this purpose. Then, such motions can be achieved by concatenation of trajectories of (15) which, at every point $x\in M$, are tangent to elements of $\mathrm{span}\{f_i, i=0,1,\ldots,m\}$ at $x\in M$. To this end, the LTP package proves helpful in determining the vector field, which over a given interval of time $T$, yields motions equivalent to any desired concatenation. More precisely, let $0=t_0<t_1<t_2<\ldots<t_s=T$ be a partition of a given interval $[0,T]$, let $\bar{\epsilon}\stackrel{def}{=}\{\epsilon_i=t_i-t_{i-1}; i=1,\ldots,s\}$, and let $\bar{u}$ be a sequence of constant controls by $\bar{u}\stackrel{def}{=}\{u^i\in\mathbb{R}^{m+1}; i=1,\ldots,s\}$ each of which is applied over $[t_{i-1},t_i]$. Additionally, let $g_i(x)\stackrel{def}{=}f(x,u^i)$, $i=1,\ldots,s$, be the vector fields constituting the right-hand sides of system (15) that correspond to $u^i$, $i=1,\ldots,s$. Employing the CBH formula (3), the package can then help to determine the vector field $\bar{f}(x,\bar{u},\bar{\epsilon})$ such that for any $p\in\mathbb{R}^n$, the solution to (15), $x^{\bar{u}}$, corresponding to the sequential application of the constant controls satisfies:

$$x^{\bar{u}}(T)=p\,e^{\epsilon_1 g_1}\cdots e^{\epsilon_s g_s} = p\,e^{T\bar{f}}~$$ (17)

where, $e^{\epsilon g}$ denotes the flow of the differential equation $\dot{x}=g$ so that $p\,e^{\epsilon g}$ is the solution of this equation with initial condition $p\in M$, evaluated at time $\epsilon$. For arbitrary $\bar{u}$, $\bar{\epsilon}$, equation (17) is guaranteed to hold only if the Lie algebra of vector fields $L(f_0,f_1,\ldots,f_m)$ is nilpotent, all the vector fields involved are real, analytic, and complete, as then the CBH formula is known to hold globally; see [29, p. 95] and [43, p. 195]. When $L(f_0,f_1,\ldots,f_m)$ is not nilpotent, the package can only provide an approximate expression for $\bar{f}$, and generally, (17) will be valid only locally, i.e. for sufficiently small $T$. A natural way to obtain such an approximation is to employ the LTP package using $L_k(\bar{X}_{m+1})$ in place of $L(\bar{X}_{m+1})$, where $L(f_0,f_1,\ldots,f_m)$ is the image of $L(\bar{X}_{m+1})$ under the evaluation map $Ev$. Under the same evaluation map $L_k(\bar{X}_{m+1})$ maps into $\textrm{\scriptsize\raisebox{.6ex}{\ensuremath{\sim}}}\hspace{-.57em}\textit{L}_k(f_0,f_1,\ldots,f_m)$, a truncated version of $L(f_0,f_1,\ldots,f_m)$.

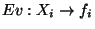
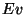
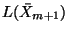
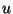
Remark 4.1   The use of $L_k(\bar{X}_{m+1})$ in place of $L(\bar{X}_{m+1})$ is a valid way to obtain an approximation of $\bar{f}$ in view of the results in [40] which also provide a link between the purely abstract algebraic formalism of Section 3 and the actual solution of (15). 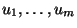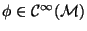More precisely, if $u$ is a Lebesgue integrable control function on $[0,T]$, then the image of the Chen-Fliess series $Ser(u)$, under the evaluation map $Ev$, $Ev(Ser(u))$, is a formal series of partial differential operators acting on smooth functions defined on the manifold $\mathcal{M}$. 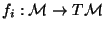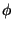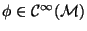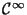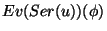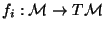If $\phi\in\mathcal{C}^{\infty}(\mathcal{M})$ then application of $Ev(Ser(u))$ to $\phi$ yields a formal series of $\mathcal{C}^{\infty}$ functions on $\mathcal{M}$ denoted $Ev(Ser(u))(\phi)$. 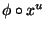In [40, Prop. 4.3, p. 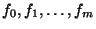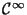698], this series is actually shown to converge to $\phi\circ x^u$, the composition of $\phi$ with the solution of system (15) corresponding to $u$. 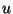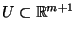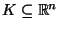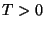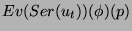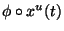Specifically, it was shown that: for analytic, complete vector fields $f_0,f_1,\ldots,f_m$, any compact set $U\subset \mathbb{R}^{m+1}$ and, any compact set $K\subseteq\mathbb{R}^n$, there exists a time horizon $T>0$ such that the formal power series $Ev(Ser(u_t))(\phi)(p)$ (evaluated at $p\in M$) actually converges uniformly to $\phi\circ x^{u}(t)$ for $t\in[0,T]$, where $x^{u}(t):[0,T]\rightarrow\mathcal{M}$ is the solution of (15), with $x(0)=p$, 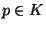for any $p\in K$, and any integrable $u:[0,T]\rightarrow U$. 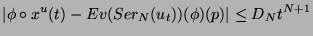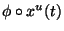Furthermore, a precise upper bound was obtained in the same reference for the difference between $\phi\circ x^{u}$ and the $N$-$th$ partial sum of the series $Ev(Ser(u_t))(\phi)(p)$ for $t\in[0,T]$:

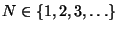$$\vert\phi\circ x^{u}(t)-Ev(Ser_N(u_t))(\phi)(p) \vert\leq D_N t^{N+1}$$ (18)

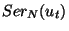
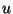
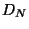
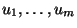
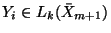
for all $N\in\{1,2,3,\ldots\}$, $p\in K$, $u$ as defined above, and all $t\in[0,T]$, where $Ser_N(u_t)$ denotes the truncated series obtained by considering terms only up to order $N$ in the Chen-Fliess series $Ser(u)$, and $D_N$ is a constant.

In view of the last remark, an ``approximation'' to $\bar{f}$ can be calculated employing the LTP package for repeated application of the CBH formula to perform formal calculations associated with the composition of the formal exponential maps on $L_k(\bar{X}_{m+1})$. Precisely, if $Y_i\in L_k(\bar{X}_{m+1})$ corresponds to $g_i$ via $Ev(Y_i)=g_i$, for $i=1,2,\ldots,s$, then repeated application of the CBH formula yields $\bar{Y}\in L_k(\bar{X}_{m+1})$ such that

$$e^{\epsilon_1 Y_1}\cdots e^{\epsilon_s Y_s}=e^{T \bar{Y}}$$ (19)

Also, it follows that $\exp(T\bar{Y})$ can be expressed as $Ser_k(\bar{u_T})$ (a partial sum $Ser(\bar{u}_T)$ containing only Lie monomials up to order $k$). Therefore, it is only in the sense of (18) that $\tilde{f}\stackrel{def}{=}Ev(\bar{Y})$ can be considered an approximation to $\bar{f}$. Note that (18) can be applied with $\phi$ as coordinate functions on $M$ which immediately implies increasing proximity of trajectories $p\,e^{t\tilde{f}}$ and $p\,e^{t\bar{f}}$ for $t\in[0,T]$, with increasing order $k$ of nilpotent truncation. Rather than using piece-wise constant controls, it is often more convenient to calculate the flows of dynamical systems such as (15) with control functions $u_i$, $i=1,\ldots,m$, which are only integrable. For this purpose, a generalized CBH formula (logarithm of the Chen-Fliess series) for nonstationary vector fields would have to be employed as mentioned in Remark 3.3. The product expansion (7) and the associated formula (14), would however still be valid.