Basic Notions and LTP Formalism

This section provides the basic notions and formalism that constitutes a general framework for calculations relevant to the behaviour and properties of dynamical systems. The LTP package relies on this formalism as it is designed to aid analysis and synthesis of systems of basically unlimited Lie algebraic structure. In lay terms, the underlying idea of this formalism is to introduce abstract, but precise algebraic constructs which, under adequately constructed mappings, project directly onto the corresponding constructs acting on manifolds on which the particular systems evolve; see for example Remark 4.1. To this end, let $\{X_1,\ldots,X_m\}$ denote a set of indeterminates. For brevity of notation, let $\bar{X}_m=(X_1,\ldots,X_m)$. Let $A(\bar{X}_m)$ denote the free associative algebra (over $\mathbb{R}$) of noncommutative polynomials in the indeterminates $X_1,X_2,\ldots,X_m$. Recall that, given a set $\bar{X}_m$, a free associative algebra on the set $\bar{X}_m$ over $\mathbb{R}$, is an associative algebra $A(\bar{X}_m)$ over $\mathbb{R}$, together with a mapping $i:\bar{X}_m\rightarrow A(\bar{X}_m)$, with the following universal property: for each associative algebra $A_0$ and each mapping $f:\bar{X}_m \rightarrow A_0$, there exists a unique homomorphism of algebras $F:A(\bar{X}_m)\rightarrow A_0$ such that $f=F\circ i$. Members of $A(\bar{X}_m)$ have the form of finite linear combinations $\sum_I a_I X_I$, where the summation is over all possible multi-indices $I=(i_1,\ldots,i_k)$, with $i_j\in\{1,\ldots,m\}$, for $j=1,\ldots,k$, $k\in\mathbb{N}$, in which the coefficients $a_I$ are real numbers. Here $X_I = X_{i_1}\cdots X_{i_k}$, and $X_{I=\emptyset}=1$, where, in general, $X_iX_j\neq X_jX_i$ as implied by noncommutativity. Let a Lie product $[X_i,X_j]$ of two indeterminates be defined as the noncommutative polynomial $X_jX_i-X_iX_j$. With this definition of the Lie product $A(\bar{X}_m)$ becomes a Lie algebra. Let $L(\bar{X}_m)$ be the subalgebra of $A(\bar{X}_m)$ generated by $\bar{X}_m$. The elements of $L(\bar{X}_m)$ are referred to as Lie polynomials. Further, let $\hat{L}(\bar{X}_m)$ denote the Lie algebra of Lie series in $X_1, \ldots,X_m$. The elements of $\hat{L}(\bar{X}_m)$ are formal series of the type $\sum_{i=1}^{\infty} a_i S_i$, where $a_i$ are coefficients in $K$ and $S_i\in L(\bar{X}_m)$. Clearly, any element $Z\in \hat{L}(\bar{X}_m)$ can be written as a formal infinite series $\sum_I a_I X_I$ in the indeterminates $X_1, \ldots,X_m$, in which $X_I$ is some monomial in $X_1, \ldots,X_m$ and $a_{I=\emptyset}=0$. For any element in $Z\in \hat{L}(\bar{X}_m)$ the formal power series

$$e^Z=\sum_{k=0}^{\infty} \frac{1}{k!}Z^k$$ (1)

is well defined because $1\notin \hat{L}(\bar{X}_m)$. Here, $Z^k$ are infinite series in the indeterminates $X_1, \ldots,X_m$ obtained by the natural multiplication rule for the component monomials of $Z$, $X_IX_J=X_{I*J}$, where $I*J$ is the juxtaposition (concatenation) of the components of the multi-indices $I$ and $J$. The set $\hat{G}(\bar{X}_m)=\{e^Z:Z\in\hat{L}(\bar{X}_m)\}$ is called the set of exponential Lie series in the indeterminates $X_1, \ldots,X_m$. Note that, due to the antisymmetry property and the Jacobi identity of the Lie product, not all the elements of a Lie algebra $L(\bar{X}_m)$ are linearly independent. A procedure to construct a basis for any Lie algebra of indeterminates, while taking into account the dependencies imposed by the antisymmetry and the Jacobi identities, involves selecting some of the Lie product of $X_1, \ldots,X_m$, which can, for example, be carried out in accordance with the rules given below, see [32,36,4].

Definition 3.1   - Hall basis (HB). Let $B$ denote the basis for $L(\bar{X}_m)$, and let $B_i$ be the $i$-th element in this basis. Let the length (order ) of a Lie product $G$, $l(G)$, be defined as the number of indeterminates in the expansion of $G$, also given recursively by:

$$\begin{eqnarray*} l(X_i)&=&1\hspace{2cm} i=1,\ldots,m\\ l([G,H])&=&l(G)+l(H) \end{eqnarray*}$$

where $G$ and $H$ are Lie products. Then a Hall basis is an ordered set of Lie products $\{B_i\}$ such that:

1. $X_i \in B,\ i=1,\ldots, m$
2. If $l(B_i)<l(B_j)$ then $B_i<B_j$
3. $[B_i, B_j] \in B$ if and only if
   1. $B_i, B_j \in B$ and $B_i<B_j$ and
   2. either $B_j=X_k$ for some $k$ or $B_j=[B_p, B_q]$ with $B_p, B_q \in B$ and $B_p\leq B_i$.

The proof that a Hall basis indeed constitutes a basis for the Lie algebra $L(\bar{X}_m)$ is found in [14,36].

Remark 3.1   The basis presented above, although already know by P. Hall, was first introduced by M. Hall [14] and pertains to one of the possible ways in which a basis for $L(\bar{X}_m)$ could be constructed. In fact, the above construction was generalized by Scützenberger [34] by weakening the degree condition 2 in Definition 3.1. Viennot, [44], further relaxed condition 2 replacing it by:

2'.

If $[B_i,B_j]\in B\setminus \bar{X}_m$ then $B_i\in B$ and $B_i<[B_i,B_j]$.

The last is so general that it includes the Lyndon basis and the Širšov basis [37], which is not the case with the original bases of M. Hall; see [30,24,25] for a comprehensive exposition of different bases constructions. The choice of the above, rather restrictive, basis construction was deliberate for the purpose of the LTP because it is the one most often used in the engineering literature. Nevertheless, it is worth noting that other bases construction using condition 2' instead of 2 could prove more advantageous in applications for which a particular choice of coordinate system is desirable. With regard to the algorithmic implementation of the package, a choice of Lyndon basis would possibly offer some advantages. A Lyndon basis is defined as a set of alphabetically ordered Lyndon words over a given alphabet $A$ (which is defined as a set of letters). A Lyndon word is any nonempty, finite sequences of letters which precedes all its nontrivial proper right factors in any alphabetically ordered set on $A$; i.e. 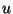$w$ is a Lyndon word if for each nontrivial factorization in terms of sub-words $u$ and $v$, $w=uv$, the word $w$ precedes $v$. From Theorem 5.1 in [30] it follows that each element of the Lyndon basis can be uniquely rewritten as an element of a Hall basis satisfying Definition 3.1 with condition 2 replaced by 2'. It is the rewriting system of [25] that provides a procedure that allows one to translate any Lyndon word into an element of a Hall basis, thus permitting to use words in place of their corresponding Lie bracket expressions. For example, given the alphabet $\{1,2,3\}$, the sequence of Lyndon words: 12, 112, 212, 1213, 1223, 3323, translates, in a one-to-one way, into the following Hall basis elements: $[X_1,X_2]$, $[X_1,[X_1,X_2]]$, $[X_2,[X_1,X_2]]$, $[[X_1,X_2],[X_1,X_3]]$, $[[X_1,X_2],[X_2,X_3]]$, $[X_3,[X_3,[X_2,X_3]]]$ in $L(\bar{X}_3)$. On the one hand, operating on words (character strings) requires less memory, but on the other hand, operations on Lie brackets (binary tree structures) can generally take less processing time than those involving words.

Let $L_k(\bar{X}_m)\subset L(\bar{X}_m)$ denote the free nilpotent Lie algebra of order $k$, i.e. a Lie algebra that can be identified with the quotient $L(\mathcal{X}_m)/I_k$, where $I_k\subset L(\bar{X}_m)$ is the ideal spanned by all elements of the Hall basis of order strictly greater than $k$. Hence, $L_k(\bar{X}_m)$ can be formed by assuming that all the Lie products in $L(\bar{X}_m)$ of degree strictly greater than $k$ are equal to zero. The above procedure can still be employed to construct bases for $L_k(\bar{X}_m)$ simply by forming all the Lie products that satisfy the above properties and whose length does not exceed $k$. By the result of Campbell, Baker, and Hausdorff, known as the CBH formula, it follows that $\hat{G}(\bar{X}_m)$ is closed under multiplication, and is in fact a group, as it can be verified that $e^Ze^{-Z}=1$, for any $Z\in\hat{G}(\bar{X}_m)$. Moreover, the map $exp:\hat{L}(\bar{X}_m)\rightarrow \hat{G}(\bar{X}_m)$ is a bijection from $\hat{L}(\bar{X}_m)$ onto $\hat{G}(\bar{X}_m)$. It follows that for any $Z_1, Z_2\in \hat{L}(\bar{X}_m)$ we can compute a unique $Z_3\in{L}(\bar{X}_m)$ such that

$$e^{Z_1} e^{Z_2} = e^{Z_3}~$$ (2)

The way to compute $Z_3$ is also delivered by the CBH formula which, in Dynkin's form, is given by [36,39]:

$$Z_3 = \sum_{m=1}^{\infty}\sum \frac{(-1)^{m-1}(ad_{Z_2})^{q_m}(ad_{Z_1}... ..._2})^{q_1}(ad_{Z_1})^{p_1}} {m\sum_{i=1}^{m}(p_i+q_i)\prod_{i=1}^{m}(p_i!q_i!)}$$

$$= Z_1+Z_2+\frac{1}{2}[Z_1,Z_2]+\frac{1}{12}([[Z_1,Z_2],Z_2]-[[Z_1,Z_2],Z_1])~$$ (3)

$$-\frac{1}{48}([Z_2,[Z_1,[Z_1,Z_2]]]+[Z_1,[Z_2,[Z_1,Z_2]]])+\dots$$

where the inner sum ranges over all $m$-tuples of pairs of nonnegative integers $(p_i,q_i)$ such that $p_i+q_i>0$. In (3), with the exception of the last term, the symbol $ad_X$ denotes the mapping $ad_X:Y\mapsto [X,Y]$ for all $Y\in L(\bar{X}_m)$, which is an endomorphism of $L(\bar{X}_m)$ underlying the adjoint representation of $L(\bar{X}_m)$, defined as the mapping $X\mapsto ad_X$. With some abuse of notation, the last term in (3) should be understood differently and must be evaluated as follows: $ad_Z^n=1$ if $n=0$, $ad_Z^n=Z$ if $n=1$, and $ad_Z^n=0$ if $n>1$. It is worth noticing that the group $\hat{G}(\bar{X}_m)$ is not a Lie group because it is infinite dimensional. As the package is primarily a tool for the analysis of dynamical systems, it will be applied in the context of groups of transformations acting on the underlying manifold on which the system evolves, see [43]. For analytic systems whose accessibility Lie algebras, [32], are finite dimensional, such groups of transformations can be given the structure of Lie groups; see [29]. It is hence helpful to define $G_k(\bar{X}_m)$, a nilpotent version of $\hat{G}(\bar{X}_m)$:

$$G_k(\bar{X}_m)\stackrel{def}{=}\{e^Z:Z\in L_k(\bar{X}_m)\}$$ (4)

The group $G_k(\bar{X}_m)$ is now a Lie group with Lie algebra $L_k(\bar{X}_m)$, see [43]. For a systematic development it is assumed here that all groups of transformations act from the right on the underlying manifolds $M$. With this notation, for $x\in M$, the expression $x e^{Z}$ denotes the value of a group action $e^Z$ at a point $x\in M$, [36, p. LG 4.11] or [43, p. 74]. One of the many applications of the LTP package involves the solution of differential equations defined on Lie groups. As will be explained later, the trajectories of these equations relate (through a Lie group homomorphism, see Remark 4.1) to trajectories evolving on $G_k(\bar{X}_m)$. It is hence convenient that $G_k(\bar{X}_m)$ is equipped with a coordinate system. Such a coordinate system can be constructed in terms of a Hall basis and has the advantage of being global (consisting of a single chart) since $G_k(\bar{X}_m)$ is nilpotent, see [41]. In full rigour, if $\{B_1,B_2,\ldots,B_r\}$ is the $r$-dimensional Hall basis for a given nilpotent Lie algebra $L_k(\bar{X}_m)$, then any element $P$ in the Lie group $G_k(\bar{X}_m)$ has the following unique representation, [20]:

$$P=e^{\gamma_1 B_1}e^{\gamma_2 B_2}\cdots e^{\gamma_r B_r}~$$ (5)

The map $P\rightarrow (\gamma_1,\gamma_2,\ldots,\gamma_r)$ establishes a global diffeomorphism between $G_k(\bar{X}_m)$ and $\mathbb{R}^r$ and is thus a global coordinate chart on $G_k(\bar{X}_m)$. The coordinate system so just introduced falls into the category of Lie-Cartan coordinate systems of the second kind [36,32]. Here, we will refer to it using the name of $\gamma$-coordinates. Equation (5) can be viewed as a way to represent an arbitrary group action as a composition of elementary group actions defined in terms of the elements of the Hall basis of the Lie algebra associated with the group. This fact has been exploited by Wei and Norman in the solution of right-invariant parametric differential equations evolving on $G_k(\bar{X}_m)$:

$$\dot{S}(t) = \left (\sum_{i=1}^{m} X_iu_i(t)\right ) S(t)~$$ (6)

$$S(0) = I %%\in G_k(\bar{X}_m)$$

where $m<\infty$ (finite), $X_i$ are indeterminate operators independent of $t$ that generate $L_k(\bar{X}_m)$ under the commutator product $[X_i,X_j]=X_jX_i-X_iX_j$, and $u_i$ are scalar functions of $t$. Here, as $S(0)\in G_k(\bar{X}_m)$, $S(t)$ evolves on $G_k(\bar{X}_m)$. Therefore, the solution to (6) is given by the product of exponentials:

$$S(t)=e^{\gamma_1(t)B_1}e^{\gamma_2(t)B_2}\cdots e^{\gamma_r(t)B_r} =\prod_{i=1}^{r}e^{\gamma_i(t)B_i}~$$ (7)

where $\{B_1,B_2,\ldots,B_r\}$ is the Hall basis for the Lie algebra $L_k(\bar{X}_m)$, and the $\gamma_i$ are scalar functions of time, see [41,45]. Without the loss of generality, it may be assumed that $B_i=X_i$, for $i=1,\ldots,m$.

Remark 3.2   The representation (7) of the solution to equation (6) is not unique. Alternatively, the solution to (6) can be represented using the Lie-Cartan coordinates of the first kind, i.e. it is possible to write

$$S(t) = e^{\left (\sum_{i=1}^{r}\theta_i(t) B_i\right )} %%~\la{singleexp}$$

where $\theta_i:\mathbb{R}\rightarrow\mathbb{R}$, $i=1,2,\ldots,r$, are the ``coordinates'' of such a solution; see [22].

Remark 3.3   For an arbitrary set of indeterminates $\bar{X}_m$ the Lie algebra $L(\bar{X}_m)$ is really infinite dimensional. A unique solution of (6), however, still exists for every Lebesgue integrable control function $u\stackrel{def}{=}[u_1,\ldots,u_m]$ defined on a finite interval $[0,T]$. This solution is known to evolve on $\hat{G}(\bar{X}_m)$, see [40, Prop. 3.1]. 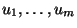Furthermore, the solution of (6) can be written in terms of a formal power series in the indeterminates $X_1, \ldots,X_m$, denoted by $Ser(u)$, and known as the Chen-Fliess series, see [12, Theorem III.2, p. 22]. 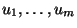The coefficients in $Ser(u)$ are iterated integrals of the control functions $u_1,\ldots,u_m$ and for any $t$, $S(t)=Ser(u_t)$, where $S(u_t)$ denotes the Chen-Fliess series with coefficients evaluated over $[0,t]$. It has been shown in [41] that the expression of the the solution of (6) in the form of a Chen-Fliess series $Ser(u_t)$ is equivalent to the expression in the form of a product of exponentials, i.e. 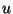for any given control function $u$, there exist functions $\gamma_{i}:[0,T]\rightarrow \mathbb{R}$, $i=1,2,\ldots$ such that (7) is valid with the product performed over all members of the P. Hall basis $\{B_i;i=1,2,\ldots\}$ for $L(\bar{X}_m)$. A particularly convenient formalism based on chronological algebras introduced for nonstationary vector fields has been introduced in [1] and permits to re-write the Chen-Fliess series in a very compact and symbolically tractable form, in which the iterated integrals are re-expressed in terms of the chronological product operations, see [18,17]. The chronological calculus has also been shown useful in the calculation of the logarithm of the Chen-Fliess series, see [31]; however, the expressions derived there, although relatively simple, provide a series expansion of this logarithm which may contain linearly dependent terms.

The $\gamma$-coordinates in (7) are shown to satisfy a set of nonlinear differential equations as is implied by the following derivation, see also [45,32]. Differentiating (7) yields,

$$\dot{S}(t)=\frac{dS(t)}{dt}=\sum_{i=1}^r \dot{\gamma}_i(t)... ...=1}^{i-1}e^{\gamma_j B_j}B_i\prod_{j=i}^r e^{\gamma_j B_j}~$$ (8)

Multiplying both sides of (8) by $S(t)^{-1}$ from the right and using the exponential formula (see [43, p. 40]):

$$(e^X)Y(e^{-X}) = Y+[X,Y]+\frac{1}{2!}[X,[X,Y]] +\frac{1}{3!}[X,[X,[X,Y]]]+\ldots$$

$$= \sum_{k=0}\frac{1}{k!}(ad_X^k)Y~$$ (9)

$$= (e^{ad_X})Y$$

yields,

$$\dot{S}(t)S^{-1}(t) = \sum_{i=1}^{r}\dot{\gamma}_i(t) \prod_{j=1}^{i-1}e^{\gamma_j ad_{B_j}}B_i~$$ (10)

 

$$= \sum_{i=1}^{r} B_iu_i(t)~$$ (11)

with $u_i(t)=0$ for $i=m+1,\ldots,r$, as $S(t)$ satisfies (6). Equating the coefficients on both sides of the last equality gives:

$$\underbrace{ \left [\begin{array}{c}u_1(t)\\ u_2(t)\\ \vdots\\ u_r(t)\end{array}\right ]}_{u} = \underbrace{ \left [\begin{array}{ccc} \xi_{11}(\gamma)&\cdots&\x... ... \dot{\gamma}_r(t)\end{array}\right ]}_{\dot{\gamma}},\hspace{5mm}\gamma(0)=0~$$ (12)

where the $\xi_{ij}(\gamma)$ are analytic functions of the $\gamma_i$'s. Clearly, $\gamma(0)=0$ since $S(0)=I$. It is worth noting that there exists a chain of ideals $0\subseteq \mathcal{I}_1 \subseteq \mathcal{I}_2 \subseteq \cdots \subseteq \mathcal{I}_r = L_k(\bar{X}_m)$ where each $\mathcal{I}_n$ is exactly of dimension $n$. The order of the elements in the Hall basis $\{B_1, \ldots, B_r\}$ is such that is the ideal $\mathcal{I}_n$ is generated by $\{B_n,\ldots,B_r\}$, which implies that the multiplication table for $L_k(\bar{X}_m)$ satisfies:

$$[B_i,B_j]=\sum_{n=i}^{r} c^{ij}_n B_n,\hspace{5mm}\textrm{for}\ i>j~$$ (13)

It can be shown, see [45], that such a multiplication table implies that $\xi(\gamma)$ is lower triangular and invertible for all $t$. Hence, (12) yields the system of differential equations for the computation of the $\gamma$-coordinates in explicit form:

$$\dot{\gamma}(t)=%%f(u,\gamma)= \xi^{-1}(\gamma)u(t),\hspace{5mm}\gamma(0)=0~$$ (14)

Equation (14) will be referred to as the Wei-Norman equation. Its solution delivers $S(t)$ of (7) which solves (6). The explicit formulæfor the solution of (14), in terms of iterated integrals, are also given in [41]; see also [18, Thm. 4.10, p. 297].