Nonlinear filtering

Lie algebraic methods originally conceived as tools for the analysis of nonlinear systems have also found application in nonlinear filtering problems; the reader is referred to [23] for a complete expository review. In the nonlinear filtering problem the objective is to estimate the state of a stochastic process $x(t)$ which cannot be measured directly, but may be inferred from measurements of a related observation process $y(t)$. Typical filtering problems consider the following signal observation model:

$$dx(t) = f(x(t))dt+g(x(t))dv(t),\hspace{5mm} x(0)= x_0$$ (20)

$$dy(t) = h(x(t))dt+dw(t), \hspace{14.9mm} y(0)= 0$$

where $x, v$ and $y, w$ are $\mathbb{R}^n$ and $\mathbb{R}^m$ valued processes, respectively, and $v$ and $w$ have components which are independent, standard Brownian processes. Furthermore, $f, h$ and $g$ are assumed to be smooth functions. Essential for the estimation of the state is the conditional probability density of the state, $\rho(t,x)$, given the observation $\{y(s); 0\leq s\leq t\}$. It is well known, see [10], that $\rho(t,x)$ is obtained by normalizing a function $\sigma(t,x)$ which is the solution of the Duncan-Mortensen-Zakai (DMZ) bilinear, stochastic, partial differential equation:

$$d\sigma(t,x) = L_0\sigma(t,x)dt + \sum_{i=1}^{m}L_i\sigma(t,x)\circ dy_i(t),\hspace{5mm}\sigma(0,x)=\sigma_0(x)$$ (21)

where $\circ dy(t)$ denotes the Fisk-Stratonovitch differential of the observation process $y(t)$, the differential operator $L_0$, given by:

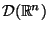$$L_0=\frac{1}{2}\sum_{i=1}^{n}\frac{\partial^2}{\partial x_i^2} -\... ...sum_{i=1}^{n}\frac{\partial f_i}{\partial x_i} -\frac{1}{2}\sum_{i=1}^{m}h_i^2~$$ (22)

is defined on the space of smooth functions $\mathcal{D}(\mathbb{R}^n)$ on $\mathbb{R}^n$ with compact support, and where $L_i$ is the operator of multiplication by $h_i$, $i=1,\ldots,m$. Here, $\sigma_0\in M_+(\mathbb{R}^n)$ is the probability density of the initial point $x_0$, and $M_+(\mathbb{R}^n)$ denotes the space of nonnegative bounded measures on $\mathbb{R}^n$. A particularly useful concept associated with the DMZ equation is the estimation Lie algebra, as introduced in [5], which is defined as the Lie algebra generated by the differential operators $L_0,\ldots, L_m$ (the Lie product of operators is calculated in a standard way, i.e. $[X,Y]\phi=X(Y\phi)-Y(X\phi)$, for any smooth function $\phi$). 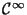The structure and dimensionality of the estimation Lie algebra is directly related to the existence of a finite dimensional recursive filter for the computation of $\rho(t,x)$, see [23]. It has been shown that if the estimation Lie algebra can be identified with a Weyl algebra of any order, then no non-constant statistics exist for the computation of the conditional density $\rho(t,x)$ with a finite dimensional filter; see references in [23]. In this context, the LTP package is helpful in the computation of the generators for the Weyl algebras as it permits to compute the Lie product in a coordinate independent fashion. In the special case when the estimation Lie algebra is finite dimensional and solvable, (see [43] for the definition of solvability), the DMZ equation can be solved via an extension of the Wei-Norman formalism. Such a construction will be illustrated by an example employing the Lie tools package.