Indexed-Sequential Files

  1. Is a B-tree of order M=4, containing all the letters of the alphabet, unique? Explain.

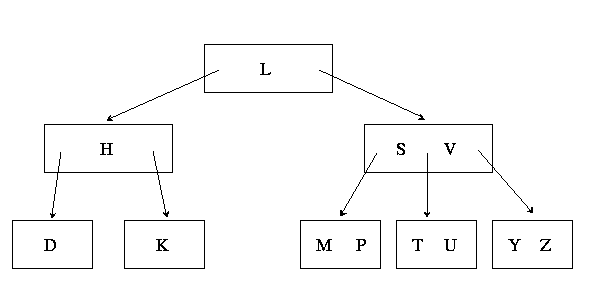
  2. For a B-tree of order 9, state the minimum and maximum number of records which may be contained in (a) the root, (b) any internal node, (c) any leaf node.

  3. A B-tree of order M=3 is given below. Insert a record with key N, making sure to show the evolution of the tree as the B-tree insertion algorithm proceeds.

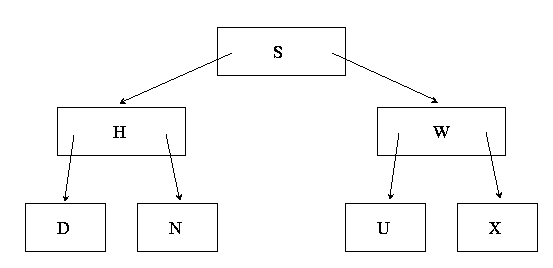
  4. A B-tree of order M=3 is given below. Delete the record with key N, making sure to show the evolution of the tree as the B-tree deletion algorithm proceeds.

  5. Why is it that the B-tree of the previous question cannot be considered a legal B+ tree?

  6. Given the following requirements, calculate the maximum order (M) of a B-tree:

  7. Calculate the maximum order of a B+ tree for a block size of 1024 bytes, a key size of 10 bytes, and a pointer size of 4 bytes.

  8. A B-tree of order M=3 allows nodes to have as many as three children. Why is a B-tree of order M=2 not necessarily a binary search tree?

  9. Given both a B-tree and a B+ tree of order M=3, consisting of three levels of completely full index nodes, how many disk accesses would it take to perform the following tasks? Fill in the table and show your calculations, below.
    task B-tree B+ tree
     at mostat least at mostat least
    locate an arbitrary record        
    locate sequentially next record        

  10. If we have a B-tree of order 10, containing keys 10 bytes in length, calculate a lower bound on the block size. Assume that all pointers are 4 bytes in length.

  11. Under what conditions would you choose a B+ tree over a B-tree?

  12. a) Construct a B-tree of order M=3 by inserting the following keys into an initially empty tree: A, B, C, D, E, F, G, H. Show the tree at each stage.

    b) Can a tree of lower height, also of M=3 and containing the same keys as in part (a) be constructed? If so, show such a tree, and if not, explain why not.

    c) If we now added a record with key I to the tree of part (a), would your answer to part (b) change? Justify your answer numerically.

    d) Delete the record with key B from the tree of part (a). Show the tree at each stage.