Fair Subdivision of Multi-Robot Tasks
School of Computer Science, McGill University


Use ← and → to navigate. Press m to see the list of slides.


Use ← and → to navigate. Press m to see the list of slides.
Small and diverse team of robots



Single Global Task
Autonomous work subdivision



A coverage task



Robots start with no information



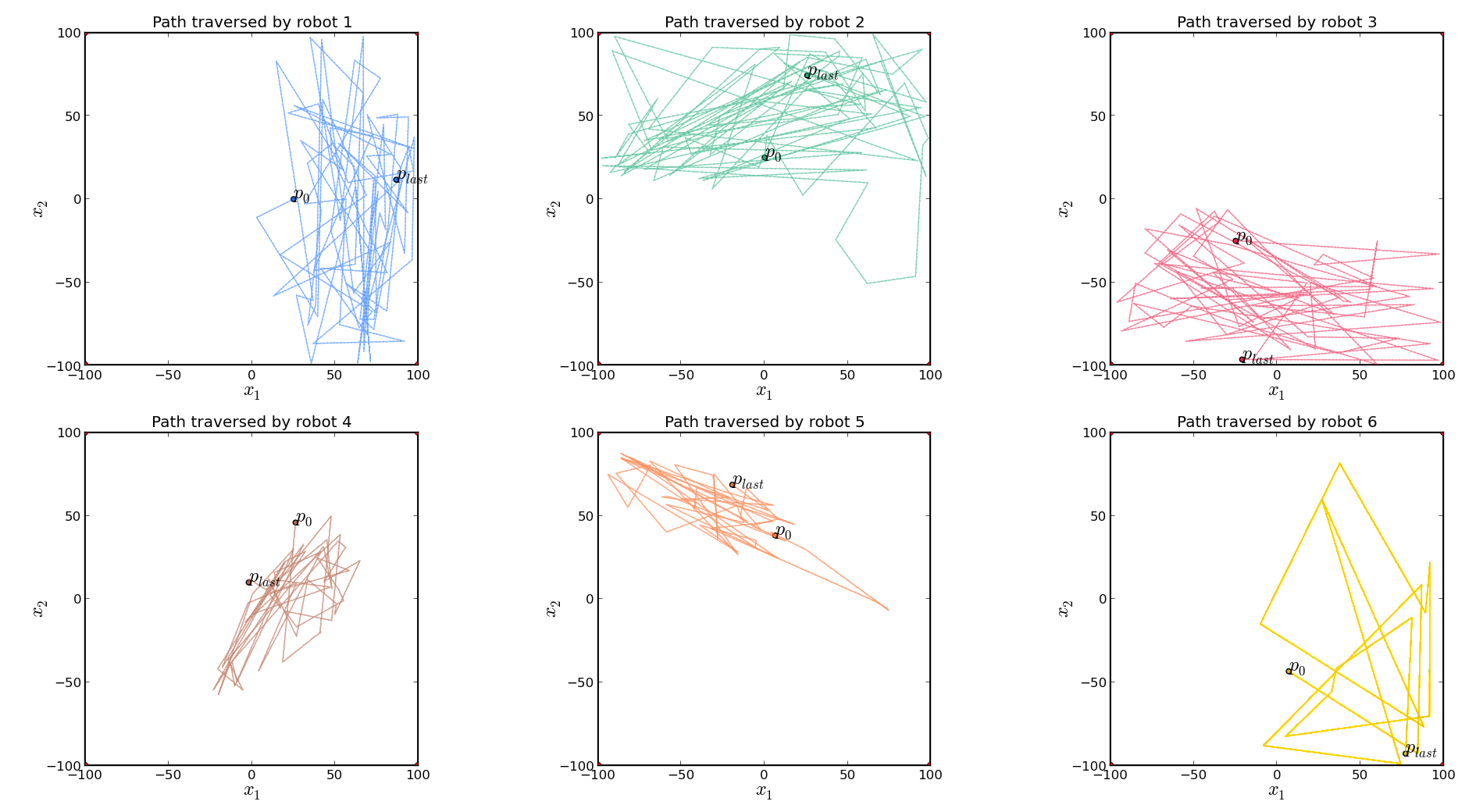
Robots agree on an allocation



But as new information comes in...
old allocation might not be the best
(bad estimates, failures, unexpected events)









[1]
L. Liu and D. Shell. (2012)
Large-scale multi-robot task allocation via dynamic partitioning and distribution.
[2]
B.P. Gerkey and M.J. Mataric.(2002)
Sold!: auction methods for multirobot coordination.
[3]
C. Rossi, L. Aldama, and A. Barrientos. (2009)
Simultaneous task subdivision and allocation for teams of heterogeneous robots.
[4]
F. Tang and L. E. Parker. (2005)
Asymtre: Automated synthesis of multi-robot task solutions through software reconfiguration.
[5]
M. Pavone, A. Arsie, E. Frazzoli, and F. Bullo (2011).
Distributed algorithms for environment partitioning in mobile robotic networks.
[6]
J. G. Carlsson. (2011)
Dividing a territory among several vehicles.
[7]
M. Schwager, M. P. Vitus, D. Rus, and C. J. Tomlin. (2011)
Robust adaptive coverage for robotic sensor networks.
[8]
S. Bhattacharya, N. Michael, and V. Kumar. (2010)
Distributed coverage and exploration in unknown non-convex environments.
Model as a fair division problem
Fair: balanced utilities and costs
Robots have a continuous "preference" over task space
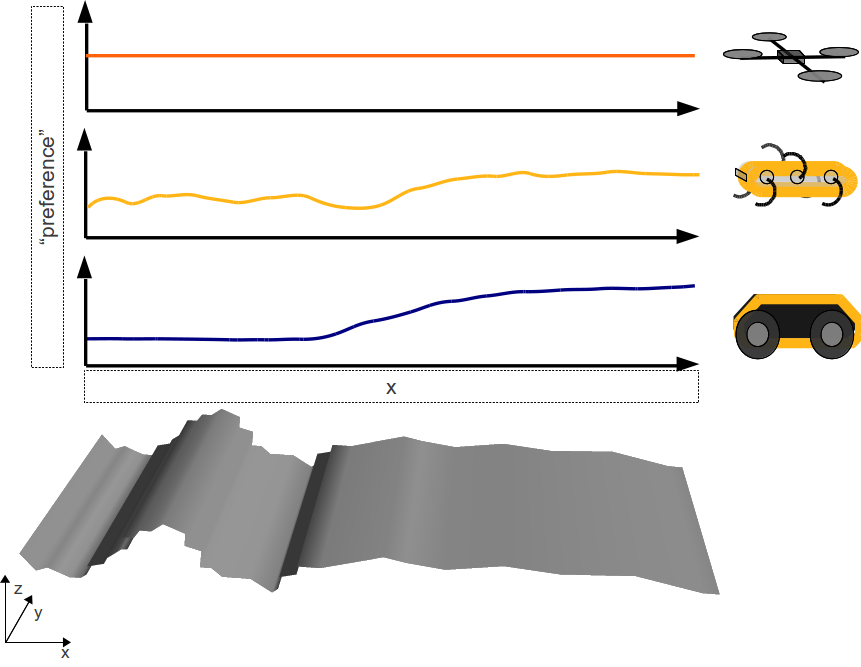
Non-zero sum game



|
|
Maximize minimum utility, with constraints on allocation sizes |
Iterative approximation algorithm for finding optimal allocations: subgradient search method (Boyd, 2003)
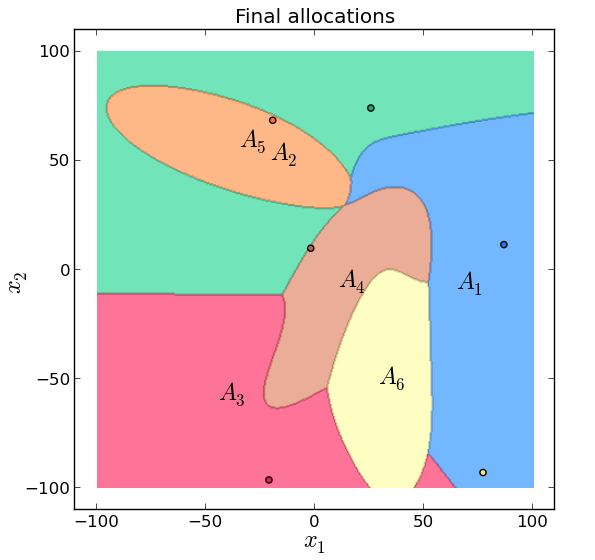
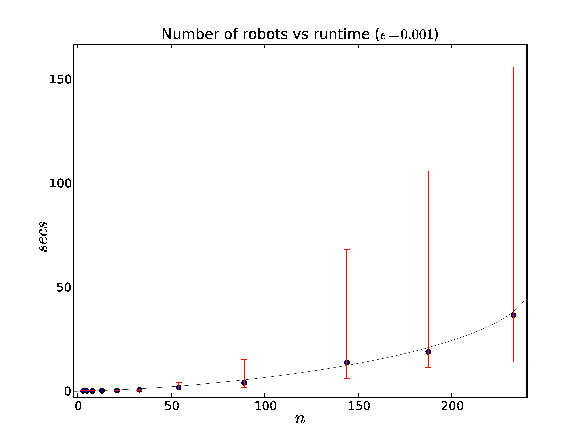
Coverage of a random polygonal region with n robots
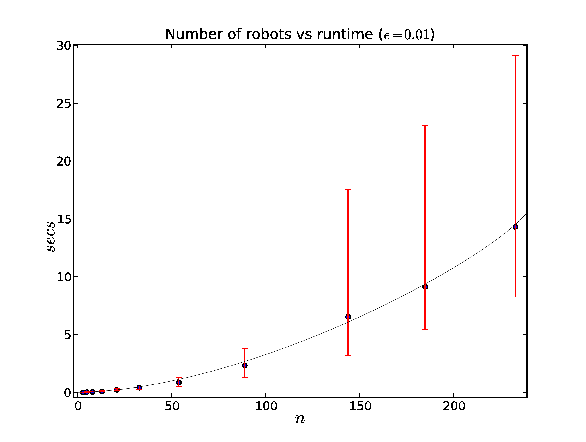
Coverage of a random polygonal region with n robots
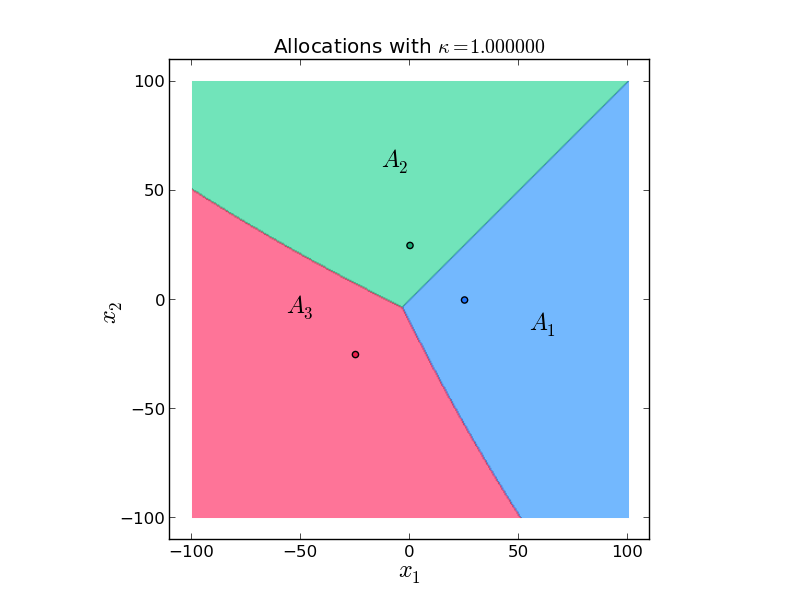
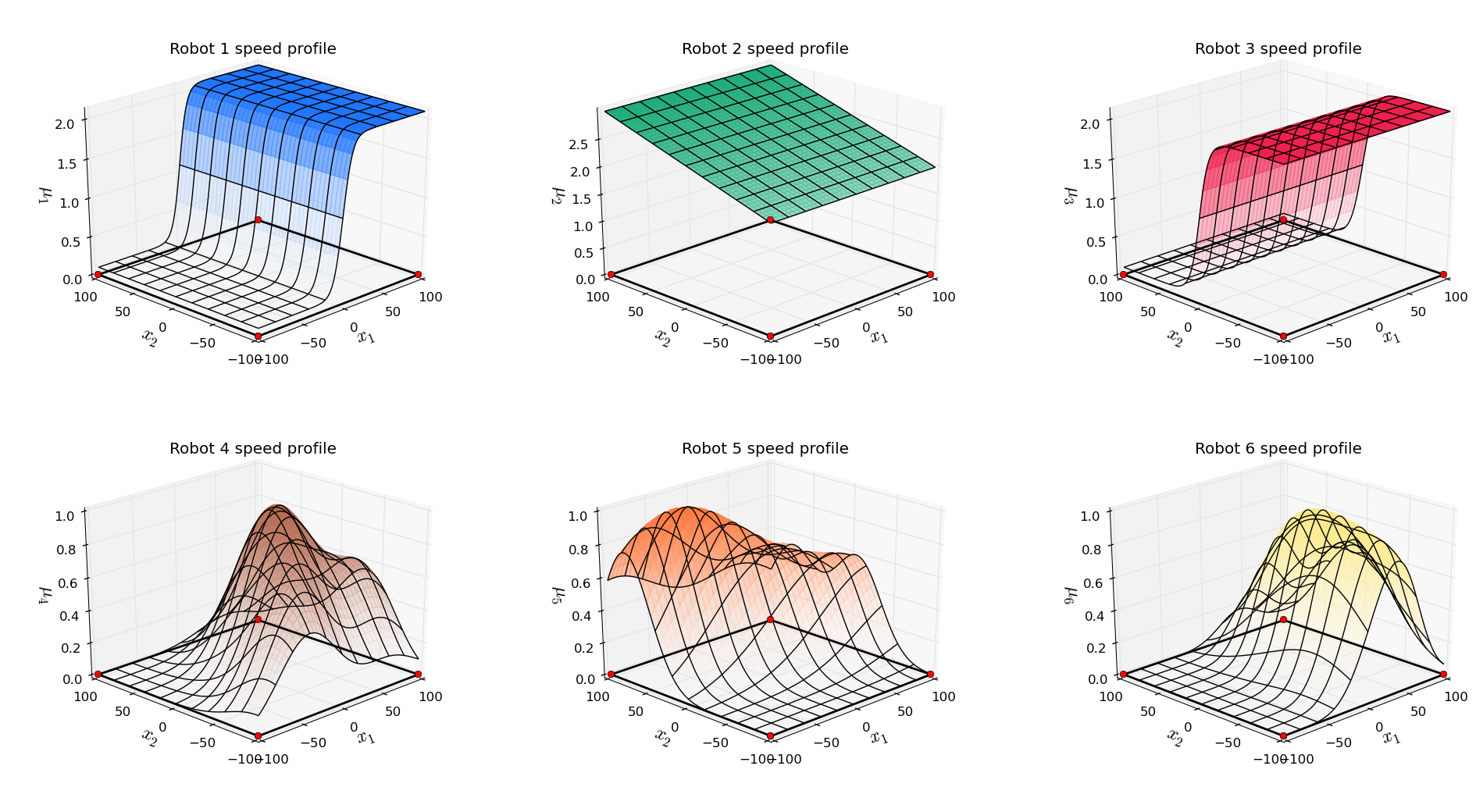
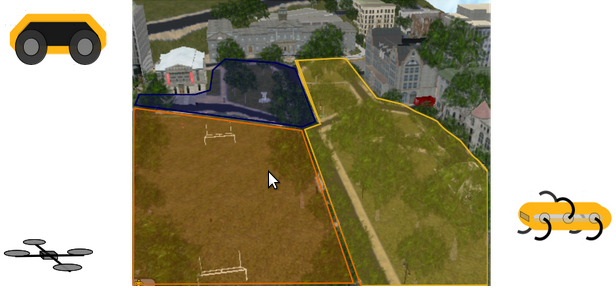
Coverage of a square region (200x200 mts) with three robots, \(f_i(x) = -\frac{1}{\textrm{speed}_i(x)} \)
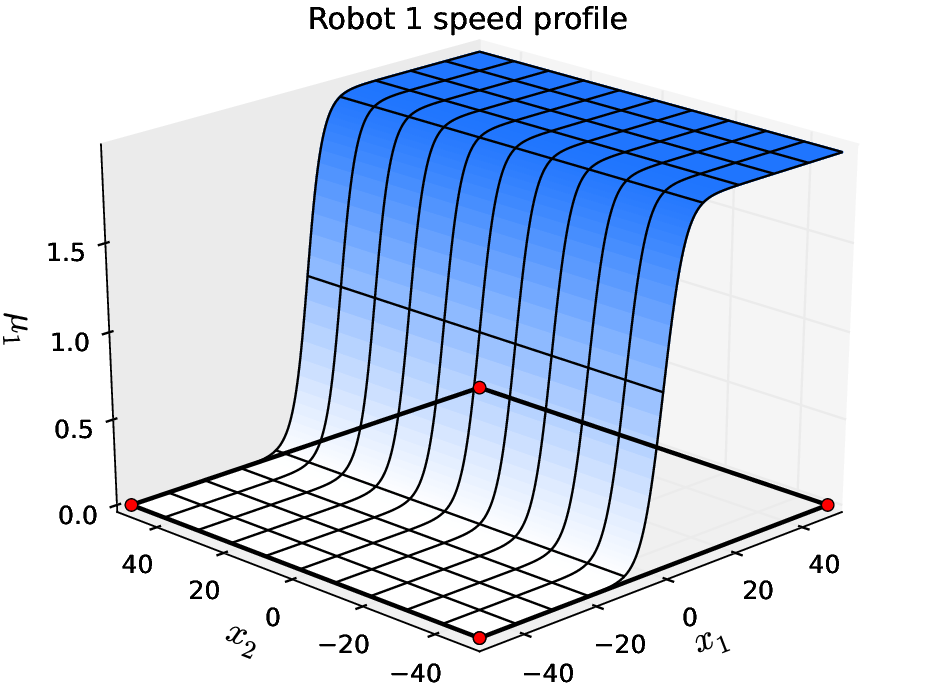
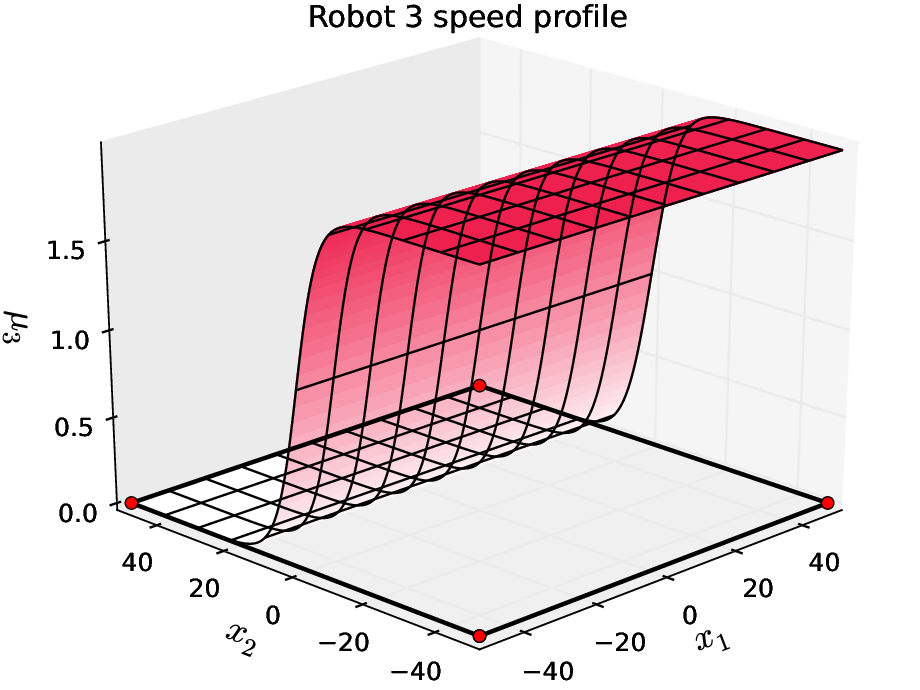
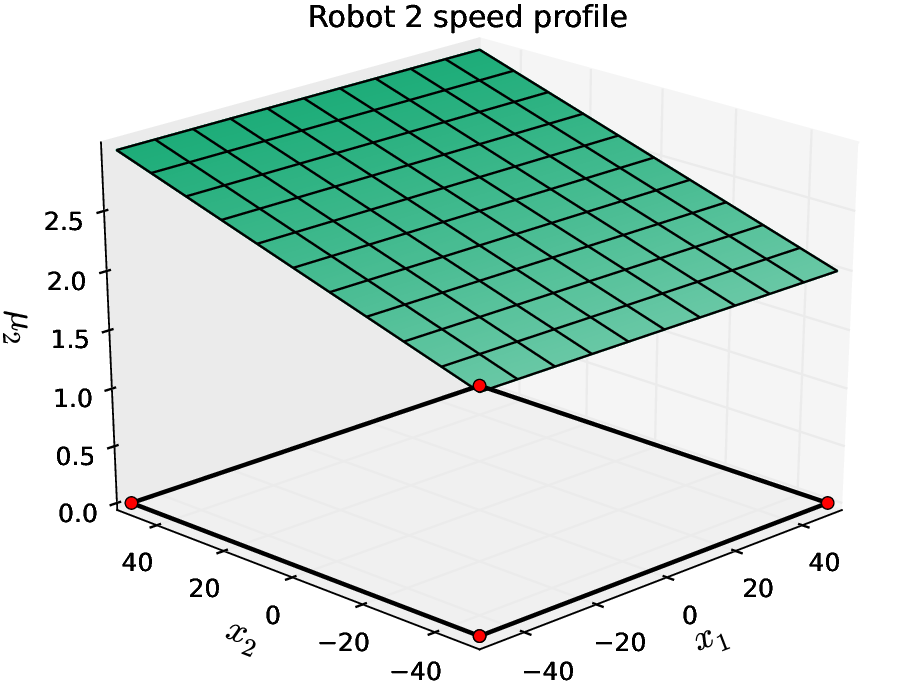

Coverage of a square region (200x200 mts) with three robots (\(p_i\) is robot i position) \(f_i(x) = - (1-k) \frac{1}{\textrm{speed}_i(x)} - k \, (\textrm{distance}(p_i,x))^2 \)
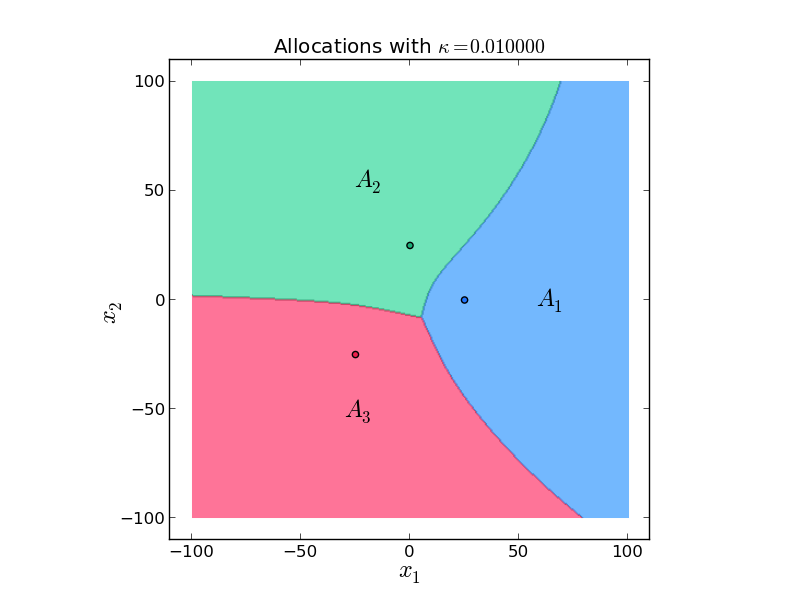
Coverage of a square region (200x200 mts) with three robots (\(p_i\) is robot i position) \(f_i(x) = - (1-k) \frac{1}{\textrm{speed}_i(x)} - k \, (\textrm{distance}(p_i,x))^2 \)
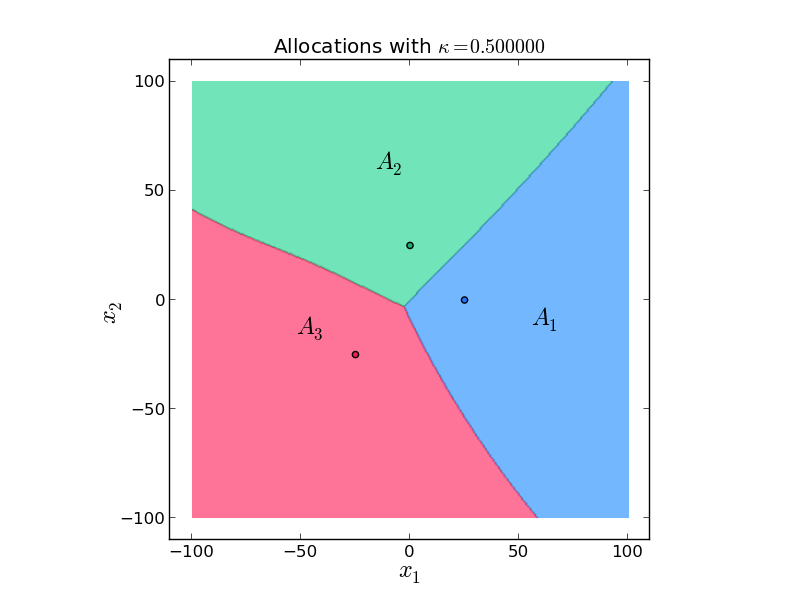
Coverage of a square region (200x200 mts) with three robots (\(p_i\) is robot i position) \(f_i(x) = - \textrm{distance}^2(p_i,x)\)