**ECSE 446/546: Realistic/Advanced Image Synthesis**
*Assignment 3: _Ambient Occlusion & Monte Carlo Direct Illumination_*
Due Sunday, October 20th, 2019 at 11:59pm EST on [myCourses](https://mycourses2.mcgill.ca/)
__17%__ (ECSE 446 / COMP 598) _or_ __12%__ (ECSE 546 / COMP 599)
We will explore Monte Carlo estimators for several direct illumination integration problems. First, you will implement estimators for two specialized direct illumination effects, ambient occlusion (AO) and reflection occlusion (RO). Afterwards, you will implement a more general direct illumination integrator with importance sampling schemes based on BRDF and spherical emitter distributions. This assignment comprises only __offline rendering tasks__.
Before starting, we recommend that you review the course material, especially slides on random sampling, Monte Carlo estimators and AO.
!!!Note:
Be sure that your project is synced up with the [online Git repo](https://github.com/ecsex46/fall-2019) by running: `git stash save && git pull && git stash pop`. See the [TinyRender docs](http://www.cim.mcgill.ca/~derek/ecse446/readme.md.html) for more information. The base code now contains `TODO(A3)` comments that you can search for using your IDE.
# Canonical Sample Warping (_20 pts_)
 You will first implementing methods to draw samples over various domains of interest to us and, here, with different distributions. Specifically, we will explore distributions of directions over the unit sphere and hemisphere. The methods you implement here will serve as building blocks later on in this (and future) assignments.
For each such distribution, you will be responsible for the implementation of __two__ routines: one to *draw* a sample proportional to the distribution, and another to *evaluate* the value of the PDF at a sample location. The `Warp` namespace in `src/core/math.h` encapsulates a set of sampling methods that accept 2D uniform canonical random variables $(u,v) \in [0,1)^2$ as input and output 2D (or 3D) warped samples $\phi(u,v)$ in the sampling domain of interest. Corresponding PDF evaluation methods are also associated to each of these sampling routines.
There are a total of four (4) distributions we will expect you to support, and so you will have to implement eight (8) warping and evaluation methods. Each warping/PDF method pair is worth __5 points__. For more information on sample warping, you can consult Chapter 13 of [PBRTe3][PBRT3].
(###) Uniform Spherical Direction Sampling (_5 pts_))
Implement `Warp::squareToUniformSphere()` and `Warp::squareToUniformSpherePdf()`: the former should transform uniform 2D canonical random numbers (i.e., on the unit square) into uniform points on the surface of a *unit sphere* (centered at the origin; i.e., unit spherical directions); the latter should implement a probability density evaluation function for this warping.
(###) Uniform Hemispherical Direction Sampling (_5 pts_))
Implement `Warp::squareToUniformHemisphere()` to transform uniform 2D canonical random numbers into uniformly distributed points on the surface of a unit hemisphere __aligned about the $z$-axis (0,0,1)__. Implement this function's probability density evaluation function, `Warp::squareToUniformHemispherePdf()`, too.
(###) Cosine-weighted Hemispherical Direction Sampling (_5 pts_))
Next, implement `Warp::squareToCosineHemisphere()` to transform 2D canonical random numbers to directions distributed on the unit hemisphere (aligned about the $z$-axis) according to a cosine-weighted density. Then implement its corresponding PDF evaluation method, `Warp::squareToCosineHemispherePdf()`.
Here, you may wish to implement `Warp::squareToUniformDiskConcentric()` first to help you for this task, if you choose to apply Nusselt's Analog.
(###) Phong Cosine-power Lobe Hemispherical Direction Sampling (_5 pts_))
Finally, implement `Warp::squareToPhongLobe()` to transform 2D canonical random numbers to directions distributed about a cosine-power distribution (i.e., a Phong BRDF lobe), again aligned about the $z$-axis. As usual, implement the corresponding PDF evaluation, `Warp:squareToPhongLobePdf()`, too.
# Ambient & Reflection Occlusion (_20 pts_)
## AO Monte Carlo Estimators (_10 pts_)
Your next task is to implement three (3) Monte Carlo estimators for Ambient Occlusion (AO) according to the following importance sampling schemes: uniform spherical direction sampling, uniform hemispherical direction sampling, and cosine-weighted hemispherical direction sampling. You can find the API you need to implement for the `AOIntegrator` in `src/integrators/ao.h`, and the algorithm should roughly follow the structure below:
1. intersect your eye rays with the scene geometry,
2. if there's an intersection `i`, compute the appropriate Monte Carlo AO estimate at this shade point: you can sample a direction in your MC estimator using the sampling routines you developed earlier,
3. when evaluating the visibility in the AO integrand of your MC estimator, take care when specifying relevant ray positions and directions; remember, all intersection routines expect world-space coordinates. Here, you will need to compute the parameters of a shadow ray based on `i.p` and `i.wi`, and
5. do not forget to divide by the appropriate PDF evaluation for your sample.
Note that you will have to limit the length of the shadow rays using a scene bounding sphere heuristic. Think about what would happen if you rendered an indoor scene with AO: any shadow ray you trace would hit a point in the scene and the final image would be completely black. To avoid this problem, **set the maximum shadow ray length to half of the scene's bounding sphere radius.** Use the `scene.aabb.getBSphere()` to retrieve this sphere and its corresponding radius.
The albedo is commonly set to 1.0 for AO (and RO).
Visually benchmark your integrator on the Cornell Box scene, using each of the three sampling methods. The different sampling methods can be selected using the appropriate `.toml` file and checking the `ESamplingType m_samplingStrategy` variable in the `ao.h` file to set the PDF and `wi` correctly (see the comments in `ao.h` for additional notes). Make sure that your code works correctly for each of the `.toml` files. Be sure to compare your output with the test images below, using 16 samples per pixel (spp).
 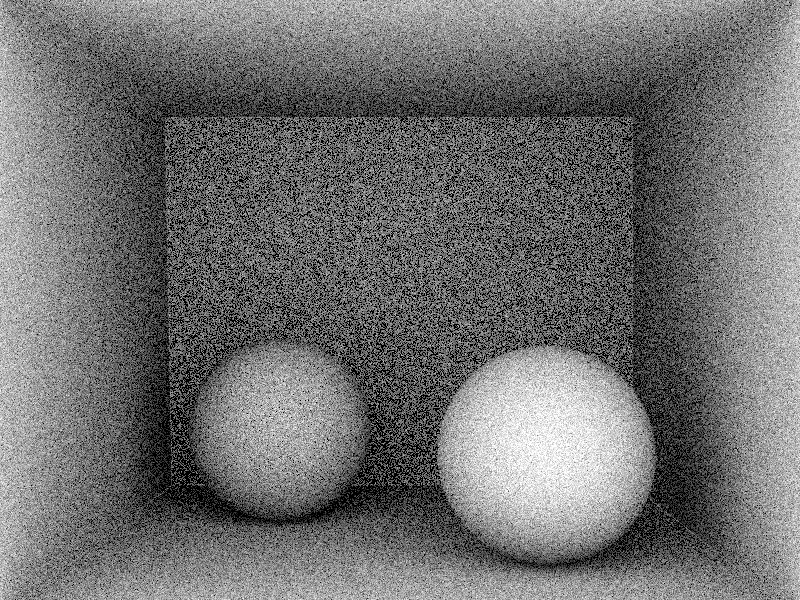 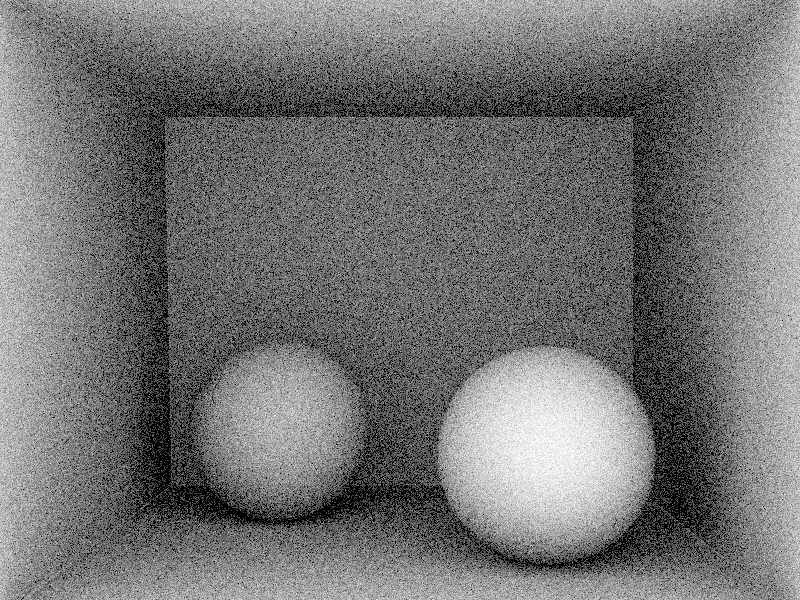
## RO Monte Carlo Estimator (_10 pts_)
Reflection Occlusion (RO) is a direct illumination effect that is similar to ambient occlusion except, instead of treating each surface as diffuse, we will associate a _Phong_ BRDF to surfaces.
Concretely, you will solve the direct illumination equation with $L_e = 1$ and $f_r = \frac{n+2}{2\pi} \max(\cos^{n}\alpha,0)$. Here, $\alpha$ is the angle formed by the mirror reflection of the view vector about the normal with the incident direction (i.e., the integration directions you will be sampling). Do not forget to account for the additional (clamped) cosine about the normal to account for foreshortening in the projected solid angle measure.
For RO, you will only be graded on the implementation of a single (1) Monte Carlo estimator using a __cosine-power lobe__ hemispherical direction sampling scheme. With that in mind, it is a good idea to first validate the correctness of your estimator by implementing other sampling schemes and seeing if images from different estimators converge to the same result (they should!).
The high-level structure of this estimator is similar to the AO estimators, with the exception of the difference in the BRDF terms. Be mindful of the various (clamped) cosine terms, and the coordinate frames the directions you will be taking scalar products need to be in. **For RO, you do not have to clamp the maximum shadow ray length.**
Implement a cosine-power importance sampled Monte Carlo estimator RO, i.e., importance sampling the Phong BRDF. Your estimator should rely on your `Warp` sampling methods. Complete the implementation of `ROIntegrator` in `src/integrators/ro.h` and render the test scene below:
![Figure [ro]: Reflection Occlusion](imgs/cbox_ro.png width=400px)
!!!Note:
Your images will not perfectly match the test images due to random noise, but there should not be any noticeable intensity differences, overall.
# Monte Carlo Direct Illumination (_60 pts_)
Before moving on to the last part of this assignment, we outline the manner in which TinyRender treats emitters.
(##) Area Lights in TinyRender
In Assignment 2 you implemented a point light source. While convenient in certain circumstances, this type of emitter is not physically realizable. In the real world, emitters have form and geometry (_e.g.,_ light bulbs, neon lights, etc.) and, in these cases, the direct illumination equation does not reduce from an integral to a singular deterministic evaluation.
(###) Emitter Structure
TinyRender has an `Emitter` structure in `src/core.h` that encapsulates the notion of an area light source. It is defined as follows:
~~~ C
struct Emitter {
size_t shapeID;
float area;
v3f radiance;
Distribution1D faceAreaDistribution;
v3f getRadiance() const { return radiance; }
v3f getPower() const { return area * M_PI * radiance; }
bool operator==(const Emitter& other) const { return shapeID == other.shapeID; }
};
~~~
|Field|Description|
|-|-|
| `shapeID`| ID of the shape the emitter is associated with |
| `area` | Total surface area of the area light |
| `radiance` | Emitted radiance (assume spatially- and directionally-uniform distributions) |
| `faceAreaDistribution` | Discrete probability density function over the mesh triangles |
When the scene description file is parsed, a vector of emitters is automatically created in `Scene`. This means that emitters are also indexed: you can have a mesh with shape ID 3 but emitter ID 0 (_e.g.,_ if there is only one light source in your scene). To determine if an intersection `i` lies on a surface emitter, you can retrieve the surface's emission with `getEmission(i)` and check if it is nonzero. Other functions you might want to use are described below; all are available from the scene.
|Method|Description|
|-|-|
| `getEmitterIDByShapeID` | Maps the shape ID to the corresponding emitter ID, if it exists |
| `getEmitterByID` | Returns a reference to an `Emitter` struct with this ID |
| `selectEmitter` | Uniformly chooses one emitter in the list of emitters (independent and identically distributed) and returns its emitter ID |
For instance, to select an emitter to sample, you can do:
~~~ C
float emPdf;
size_t id = selectEmitter(sampler.next(), emPdf);
const Emitter& em = getEmitterByID(id);
~~~
where `emPdf` is the PDF for selecting among the emitters in the scene. In our case, this is just $1/N$ for $N$ light sources. Later, you will need to multiply the light source PDF (_e.g._, `1/area`) by the probability of _choosing_ that emitter (`emPdf`) before evaluating the emitted radiance. This is due to the fact that the process of _selecting_ a light to sample is also part of the stochastic process.
You will be using the `Emitter` interface throughout this assignment. You are encouraged to look at the function signatures related to emitters to understand how they fit into the broader rendering framework.
(###) Handling Spherical Lights
In TinyRender, there are no analytic sphere shapes, only triangle meshes. In this assignment, however, __we will assume that all lights are spherical,__ so how does TinyRender handle this? To avoid creating additional structures for analytic shapes, it is possible to _convert_ tesselated meshes to analytic spheres. If `em` is known to be an emissive surface, you can retrieve its center and radius as follows:
~~~ C
v3f emCenter = scene.getShapeCenter(em.shapeID);
float emRadius = scene.getShapeRadius(em.shapeID);
~~~
Once you have these quantities, you can essentially treat the mesh as an analytic sphere to specialize your sampling strategies (_e.g.,_ solid angle or surface area). This will come in handy in Part 3.4 of the assignment. Note that your intersection tests will still rely on the tesselated mesh. **It is thus possible to sample a point on the analytic sphere but have the corresponding ray not intersect the tesselated mesh, and you need to handle this**. Before moving on to these sampling schemes, we will explore a simpler MC estimator for direct lighting.
## A Simple Direct Illumination MC Estimator (_10 pts_)
Here, you will implement a simple direct illumination integrator that uses area lights: as discussed in class, we may draw samples according to directions or points. Recall the reflection equation, which expresses the reflected radiance distribution as an integral over, e.g., the unit hemisphere centered at $\mathbf{x}$ of the product of these terms: the BRDF, the cosine foreshortening term and the incident radiance:
\begin{equation}
L_r(\mathbf{x},\omega_r) = \int_{\mathcal{H}^2} L_i(\mathbf{x},\omega_i) \, f_r(\mathbf{x},\omega_i,\omega_r) \, \cos\theta_i \, \mathrm{d}\omega_i. \label{reflec}
\end{equation}
You will approximate this integral using Monte Carlo estimation, considering only _direct_ illumination; this means that $L_i(\mathbf{x},\omega_i)$ is only non-zero for rays $\mathbf{r}(t) = \mathbf{x} + t\omega_i$ that happen to hit a light source.
A correct but naive way of estimating the reflection equation is to sample directions uniformly over the (hemi)sphere. While a good baseline to start with for validation purposes, your first estimator will instead implement __cosine-weighted hemispherical importance sampling.__ The function `DirectIntegrator::renderCosineHemisphere` (`src/integrators/direct.h`) will draw samples using `DirectIntegrator::sampleSphereByCosineHemisphere` (which you need to implement), and return an MC estimate which will once again rely on: sampling directions, tracing shadow rays from your shading point in order to evaluate the visibility in these directions, evaluating the remaining terms of the integrand at these directions, and dividing by the appropriate sampling PDF.
Implement this Monte Carlo estimator and render the test scenes `sphere_cosine_N.toml` for two setting of the sampling rate $N$ (available as the variable `m_bsdfSamples`) $N \in \{4,64\}$ in `data/a3/sphere/tinyrender`. Make sure to compare with the references below before moving onto the next part.
![Figure [sphere_hem_4]: Cosine-hemispherical sampling at 1 spp with 4 emitter samples](imgs/sphere_cosine_4.png) ![Figure [sphere_hem_32]: Cosine-hemispherical sampling at 1 spp with 64 emitter samples](imgs/sphere_cosine_64.png)
Note that this hemispherical estimator can be extremely inefficient: light sources may only subtend a small solid angle, and so many hemispherical samples can be wasted, causing the algorithm to produce noisy images at low (and even moderate) sample counts. We will soon see how to mitigate this problem with better sampling routines.
## BRDF Importance Sampling (_15 pts_)
Next, you will implement methods to directly sample the two material models we have seen so far: diffuse and Phong BRDFs. In Part 1, you implemented functions to sample different distributions and evaluate their associated probability density functions. Now, you will write methods to sample a direction in a BRDF lobe and evaluate the corresponding PDF in that direction. These two functions are part of the `BSDF` structure, which both `DiffuseBSDF` and `PhongBSDF` inherit from.
The function `BSDF::sample()` takes as input an intersection point (in local coordinates), a 2D uniform canonical random variables, and a pointer to a PDF value it will populate as output. Your goal is to sample a direction $\omega_i \sim f_s(\mathbf{x},\omega_i,\omega_o)$ and compute its density $p(\omega_i)$, before returning the evaluation of the BRDF. You need to also implement the `BSDF::pdf()` method, as you might sometimes need to separately _evaluate_ the PDF in a direction.
(###) Diffuse Reflectance BRDF (_5 pts_))
Start by implementing `DiffuseBSDF::sample()` and `DiffuseBSDF::pdf()` in `src/bsdfs/diffuse.h`. These functions both return zero for now; you have to sample a direction according to a __cosine-weighted hemispherical distribution__ and evaluate the BRDF in this direction. Use your warping functions from Part 1 in `src/core/math.h`.
(###) Phong Reflectance BRDF (_10 pts_))
Next, implement `PhongBSDF::sample()` and `PhongBSDF::pdf()` in `src/bsdfs/phong.h`. Once again, you will use the functions you implemented above to warp 2D samples to 3D directions (e.g., `Warp::squareToPhongLobe()`). Since you need to return the Phong evaluation divided by the PDF, you can call `PhongBSDF::eval()` and `PhongBSDF::pdf()` inside `PhongBSDF::sample()`. Make sure that this division is well-defined, otherwise simply return zero.
When we implemented the `PhongBSDF::eval()` function in the Phong model for A2, it combined diffuse and glossy terms. This will also have to be reflected in your sampling function. The Phong model we are implementing in TinyRender is a type of BRDF known as a _mixture model_ as it combines both diffuse and glossy (e.g., Phong) reflection effects, i.e., $~f_r = \rho_d ~ f_r^{\text{diffuse}} + ~\rho_s ~ f_r^{\text{glossy}}$. These models are useful, allowing you to augment glossy reflections with a diffuse "base coat": any reflected light that falls sufficiently outside the glossy lobe/highlight will not result in an entirely black appearance.
To do this, we can leverage a stochastic interpretation of the mixture: you stochastically choose between performing _either_ a diffuse _or_ glossy reflection event at each BRDF sampling decision. Then, depending on your stochastic choice, apply the appropriate importance sampling scheme.
For example, for a mixture model that's 50% diffuse and 50% glossy, instead of evaluating a BRDF that's a weighted sum of these lobes, you'll use a stochastic decision that will treat the reflection as a purely (i.e., 100%) diffuse reflection 50% of the time, and as a purely (i.e., 100%) glossy reflection the other 50% of the time (on average). When you choose to reflect diffusely, you will use __cosine-weighted importance sampling__; otherwise, __cosine-power (Phong lobe) importance sampling__ for the glossy case. Remember, you will need to take into account the probability of choosing that type of sampling when you do the reweighting of the contribution within the PDF evaluation.
Instead of always assuming a 50/50 split between diffuse and glossy reflection in the mixture, use the diffuse ($\rho_d$) and glossy ($\rho_s$) reflection coefficients as their respective weights. These weights are normalized, i.e., $\rho_d + \rho_s = 1$. The weight (probability) for specular sampling is given as `specularSamplingWeight`. The diffuse weight can be calculated as `1.0f - specularSamplingWeight`.
## Direct Illumination with BRDF Importance Sampling (_10 pts_)
To test your BRDF sampling routines, implement `DirectIntegrator::renderBSDF` in `src/integrators/direct.h`. Your implementation should be similar to your MC estimator from Part 3.1, except directions will now be sampled according to the BRDF lobes. Do not forget to once again use the variable `m_bsdfSamples` to determine how many samples to use. When complete, render the two test scenes `sphere_bsdf_diffuse.toml` and `sphere_bsdf_phong.toml` in `data/a3/sphere/tinyrender`. Your results for the diffuse BRDF scene should match your renders from Part Part 3.1. Your outputs for the Phong BRDF should be similar to the ones below:
![Figure [sphere_diffuse_4]: Phong BSDF sampling at 1 spp with 4 BSDF samples](imgs/sphere_bsdf_phong_4.png) ![Figure [sphere_diffuse_32]: Phong BSDF sampling at 1 spp with 64 BSDF samples](imgs/sphere_bsdf_phong_64.png)
## Direct Illumination with Emitter Importance Sampling (_25 pts_)
We will consider 2 ways of sampling spherical light sources. For both of these, use the variable `m_emitterSamples` to determine the number of emitter samples to take when rendering your images.
(###) Uniform Surface Area Sampling (_10 pts_))
Instead of sampling directions on the hemisphere, we can sample *surface points* directly on the light source. Conceptually, this means that we can express our integral using the surface area form of the reflection equation, integrating over the light source surfaces $\mathcal{A}_e$ instead of over the hemisphere of incident lighting directions $\mathcal{H}^2$:
\begin{equation}
L_r(\mathbf{x},\omega_r) = \int_{\mathcal{A}_e} L_e(\mathbf{y},\mathbf{y}\to\mathbf{x})\,f_r(\mathbf{x}, \mathbf{x}\to\mathbf{y},\omega_r) \, G(\mathbf{x} \leftrightarrow \mathbf{y}) \, \mathrm{d}\mathbf{y}, \label{area}
\end{equation}
where $G$ is the geometry term discussed in class. Here $\mathbf{x} \to \mathbf{y}$ refers to the normalized direction from $\mathbf{x}$ to $\mathbf{y}$, and $L_e(\mathbf{y},\mathbf{y} \to \mathbf{x})$ is the amount of emitted radiance in the direction $\mathbf{y} \to \mathbf{x}$. Implement the area sampling scheme in `sampleSphericalEmitter()` by sampling a position $\mathbf{y}$ on the sphere and evaluating the PDF at that point. You will need to set the direction $\omega_i = \mathbf{x} \to \mathbf{y}$, the normal at $\mathbf{y}$, and the corresponding PDF. Then, implement the MC estimator for this strategy in your `DirectIntegrator`.
![Figure [area_diag]: Surface area sampling. Green points can return nonzero radiance depending on the visibility, whereas red points are not visible from the shading point and thus contribute zero (due to $G$).](imgs/area_diagram.png width=500px)
Implement `DirectIntegrator::renderArea()` in `src/integrators/direct.h` using this sampling scheme. You will need to implement `sampleSphereByArea()` to draw samples uniformly on the sphere light.
This surface area sampling strategy is typically preferable to uniform hemispherical sampling, but roughly half of the surface samples end up being wasted (*i.e.*, falling on the backside of the sphere light, from the point of view of a shading point). Indeed, any sample on the emitter that is not directly visible from the shading point $\mathbf{x}$ will not contribute to the integral (red points in the figure, above). There is another, more efficient option for sphere light sampling.
(###) Subtended Solid Angle Sampling (_15 pts_))
To avoid generating samples on the light that will not contribute to our estimator, you will implement subtended solid angle sampling in `DirectIntegrator::renderSolidAngle()`. Sample directions towards the cone of directions subtended by the spherical light in `DirectIntegrator::sampleSphereBySolidAngle()`, setting the appropriate output fields. As before, [PBRTe3 Chapter 14.2](http://www.pbr-book.org/3ed-2018/Light_Transport_I_Surface_Reflection/Sampling_Light_Sources.html) can serve as a useful reference, here.
![Figure [sa_diag]: Subtended solid angle sampling. Every direction sampled will result in a front-facing point on the emitter.](imgs/solid_angle_diagram.png width=500px)
!!! Note:
Make sure to handle the case where your rays do not intersect the emitter: we _tesselate_ emitters to simplify the code, but your sampled directions are based on _analytic_ shapes. This can (and will) lead to discrepancies along the silhouette edges of the emitters, for both emitter sampling schemes above.
(###) Comparing Sampling Strategies
Compare your results with the reference images below. It is important to note that, in the context of spherical lights, surface area sampling will always result it more variance (noise) than subtended solid angle sampling, at equal sampling rates.
![Figure [sphere_area]: Surface area sampling at 64 spp with 1 emitter sample](imgs/sphere_area.png) ![Figure [sphere_sa]: Subtended solid angle sampling at 64 spp with 1 emitter sample](imgs/sphere_sa.png)
(#) What to submit
Render all the scenes in the `data/a3` directory. When complete, edit the `config.json` file with your credentials and submit all your code in a `.zip` archive file. Please create a _separate_ directory with only the files you need to submit, and compress this directory -- this is different than selecting all files to submit and right-clicking compress. Include your raw `.exr` files in separate folders (see the structure below).
~~~ Bash
a3_first_last.zip
config.json
src/
offline/
spaceship_ao_sphere.exr
spaceship_ao_hemisphere.exr
spaceship_ao_cosine.exr
spaceship_ro.exr
teapot_cosine.exr
teapot_bsdf.exr
teapot_area.exr
teapot_solid_angle.exr
~~~
!!! Note:
Make sure your code compiles and runs before submitting! __Code that does not compile or does not follow this exact tree structure may result in a score of zero.__ If your assignment does not compile at the moment of submission, but you do have some correct images from previous iterations, please submit these. You can use the [`tree`](https://linux.die.net/man/1/tree) command to verify this structure.
[PBRT3]: http://www.pbrt.org